Fermats sista teorem säger att det inte finns någon icke-trivial (dvs talet 0) heltalslösning för för ekvationen an + bn = cn för n större än 2.
Har inte tänkt på det innan men teoremets omvändning: det finns en heltalslösning just för n=2, är en av mina matematikfavoriter. Har framgångsrikt lärt ut det till alla mina barn kring 10-årsåldern. Poängen är att det har praktisk tillämpning då det låter en konstruera en rät vinkel med hjälp av vad som helst som går att dela upp i mått, som ett rep. Något redan de antika egyptierna kände till när de byggde pyramiderna.
Anledningen att så många har problem med matematikundervisningen är att den tjatar multiplikationstabeller och enkel aritmetik i åratal. Man borde gå snabbt vidare till intressanta grejer istället. Särskilt nu när vi har datorer så är det matematiska idéer och förståelse som borde läras ut, inte basala räkneförmågor.
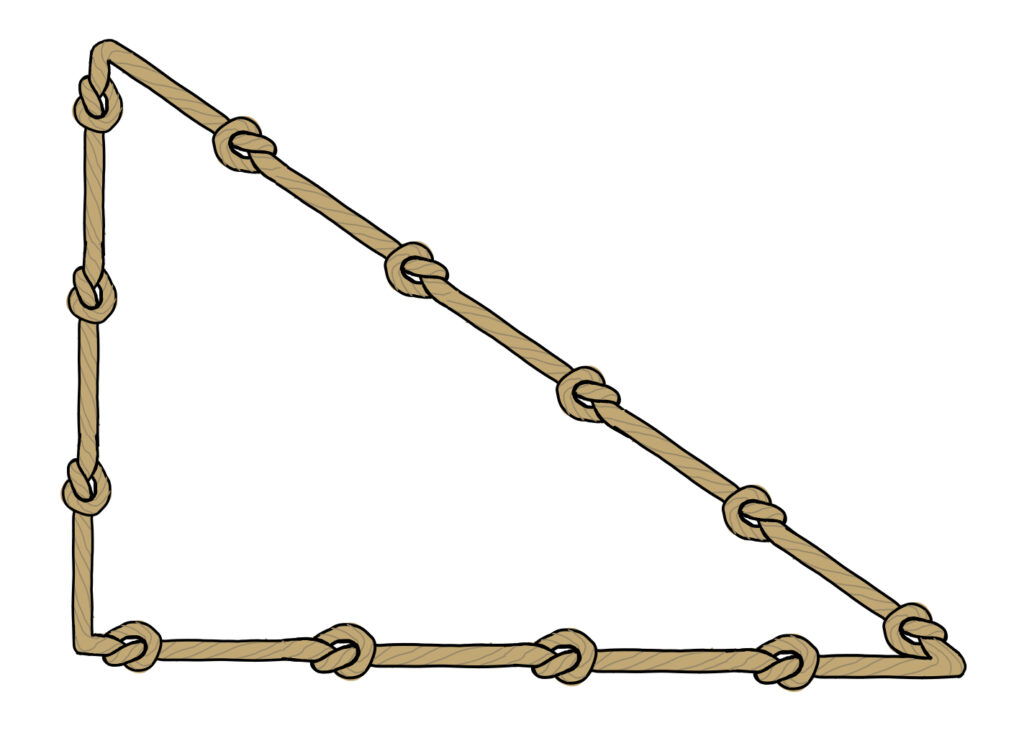
3-4-5